Алгоритм «Ханойська вежа»
Одна із прадавніх легенд говорить: «У непрохідних джунглях недалеко від міста Ханоя є храм бога Брами. У ньому перебуває бронзова плита із трьома алмазними стрижнями. На один зі стрижнів бог при створенні миру нанизав 64 диски різних діаметрів із чистого золота. Найбільший диск лежить на бронзовій плиті, а інші утворюють піраміду, що зужується догори. Це вежа Брами. Працюючи день і ніч, жерці храму переносять диски з одного стрижня на інший, дотримуючись законів Брами:
1) диски можна переміщати з одного стрижня на іншій тільки по одному;
2) не можна класти більший диск на менший;
3) не можна відкладати диски убік, при перенесенні дисків з одного стрижня на інший можна використовувати проміжний третій стрижень, на якому диски повинні перебувати теж тільки у вигляді піраміди, що зужується догори.
Коли всі 64 диска будуть перенесені з одного стрижня на іншій, настане кінець світу».
Ця прадавня легенда покладена в основу завдання про Ханойську вежу: перемістити n дисків зі стрижня 1 на стрижень 3, використовуючи проміжний стрижень 2 і дотримуючи законів Брами.
Якщо вежа складається з одного диска, то він переноситься за один хід: 1->3.
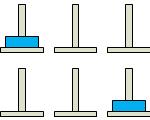
Вежа із двох дисків переноситься за три ходи: 1—>2, 1->3, 2->3.
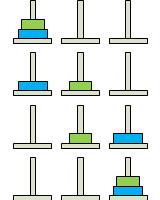
Для переносу вежі із трьох дисків буде потрібно вже сім ходів: 1->3, 1->2, 3->2, 1->3, 2->1, 2->3, 1->3. Зверніть увагу, за перші три ходи ми переносимо вежу із двох верхніх дисків на другий проміжний стрижень. Потім переносимо найбільший диск із першого стрижня на третій і ще раз проробляємо добре знайому нам операцію: переносимо вежу із двох дисків на третій диск.
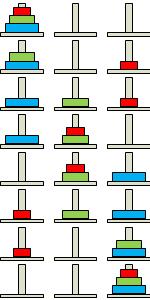
Отже, щоб перенести вежу із чотирьох дисків з першого стрижня на третій, необхідно діяти за планом:
1) перенести вежу із трьох верхніх дисків з першого стрижня на другий (7 ходів);
2) найбільший диск перенести з першого стрижня на третій (1 хід);
3) перенести вежу із трьох дисків із другого стрижня на третій (7 ходів).
Усього на перенос буде потрібно 15 ходів.
Міркуючи аналогічним образом, порахуємо число ходів, необхідних для переносу вежі з п’яти дисків: 15 + 1 + 15 = 2 * 15+ 1 = 31.
Для вежі з 6 дисків одержуємо: 2 * 31 + 1 = 63 і т.д.
Розглянутий нами алгоритм рішення завдання «Ханойська вежа» має одну дивну властивість: у ході його виконання для вежі, що полягає з n кілець, ми використовуємо алгоритм для трохи більш простої ситуації — переносу вежі, що полягає з n – 1 кільця. У свою чергу, в алгоритмі для вежі з n – 1 кільця використовується цей же алгоритм для n – 2 кілець і т.д.
Примітка, коли деякий процес описується через самого себе, то він називається рекурсією. Алгоритм рішення завдання «Ханойська вежа» — приклад рекурсивного алгоритму.